Makul bir üst sınır bulma:
Doğrusal üç noktadan bir çember geçmez ve doğrusal olmayan üç noktadan geçen biricik bir çember vardır. Bu nedenle iki farklı çember en fazla iki noktada kesişebilir.
$n$ tane çemberden iki çember seçme sayısı $C(n,2)$ olduğundan ve farklı iki çember en fazla iki noktada kesişebildiğinden $n$ farklı çember en fazla $$2\cdot C(n,2)=2\cdot \frac{n\cdot(n-1)}{2}=n\cdot (n-1)$$noktada kesişebilir.
Peki bu üst sınır her zaman sağlanır mı?
Sağladığını göstereceğimiz çember ailesi:
Yarı çapı $n$ ve merkezleri $$(0,0),\ (1,0),\ \cdots,\ (n-1,0)$$ olan çemberlerin bu üst sınırı sağladığını gösterelim.
$n=5$ özel durumu için bu çember ailesi aşağıdaki gibi olur.
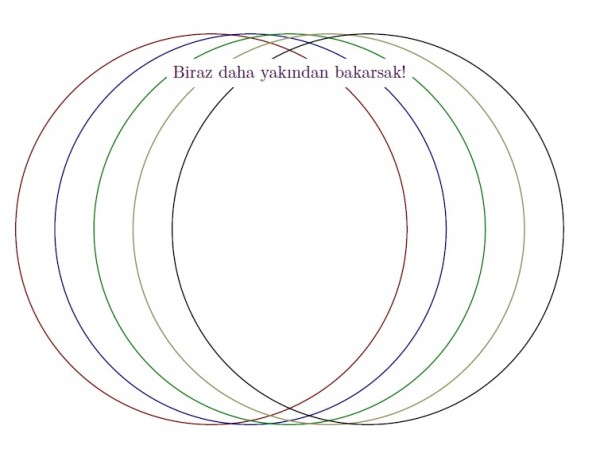
Bu çemberler iki farklı noktada kesişir:
$0\le k_1 < k_2 \le n-1$ tam sayıları için $(x_0,y_0)$ noktasının $$(x-k_1)^2+y^2=n^2 \;\;\; \text{ ve } \;\;\; (x-k_2)^2+y^2=n^2$$ denklemlerini sağladığını varsayalım. Bu noktayı denklemlere koyarsak ve taraf tarafa fark alırsak $$(x_0-k_1)^2-(x_0-k_2)^2=0 \ \ \ \text{ yani } \ \ \ (k_2-k_1)\cdot(2x_0-k_1-k_2)=0$$ eşitliği sağlanır. $k_2\ne k_1$ olduğundan $$x_0=\frac{k_1+k_2}{2}$$ eşitliği sağlanmalıdır. Bulduğumuz bu $x_0$ değerine karşılık gelen $y_0$ değerleri, birinci çemberin denklemi ile hesaplayabiliriz, $$ \sqrt{n^2-\left(\frac{k_2-k_1}{2}\right)^2}\ \ \ \text{ ya da } \ \ \ -\sqrt{n^2-\left(\frac{k_2-k_1}{2}\right)^2}$$ olur. Bu noktalar ikinci çemberin denklemini de sağlar ve kök içerisindeki ifadeler sıfıra eşit olmadığından iki farklı kesişim noktası elde etmiş oluruz.
Bu noktalardan geçen sadece iki çember vardır:
Elde ettiğimiz noktalar $x$-eksenine göre simetrik olduğundan sadece $y$ değerlerinin pozitif olduğu noktalarla ilgilenelim.
$1\le k_1<k_2 < n$ ve $1\le k_3<k_4<n$ tam sayıları için $$\left( \frac{k_1+k_2}{2}, \sqrt{n^2-\left(\frac{k_2-k_1}{2}\right)^2} \right)=\left( \frac{k_3+k_4}{2}, \sqrt{n^2-\left(\frac{k_4-k_3}{2}\right)^2} \right)$$ eşitliklerinin sağlandığını varsayalım. Bu durumda $$k_1+k_2=k_3+k_4 \ \ \ \text{ ve } \ \ \ k_2-k_1=k_4-k_3$$ sağlanır. Eşitlikleri taraf tarafa toplar ve çıkartırsak $$k_1=k_3 \ \ \ \text{ ve } \ \ \ k_2=k_4$$ eşitliklerinin sağlandığını görürüz.
Bu da ispatı bitirir ve üst sınırı sağlayan bir çember ailesi bulmuş oluruz.