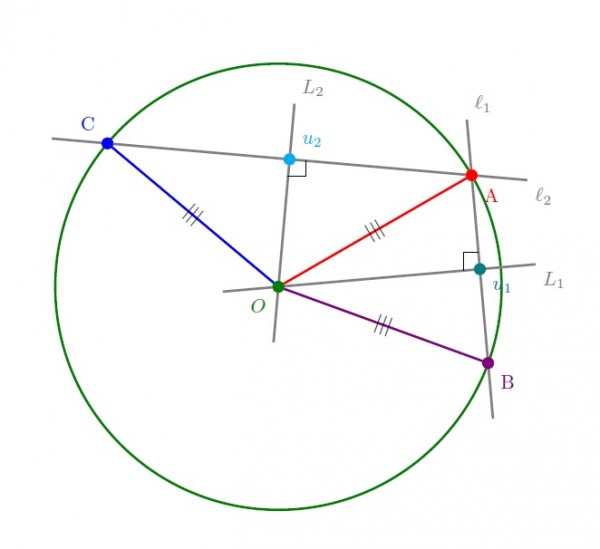
Analitik geometri ya da geometri bilgileri ile bir ispat:
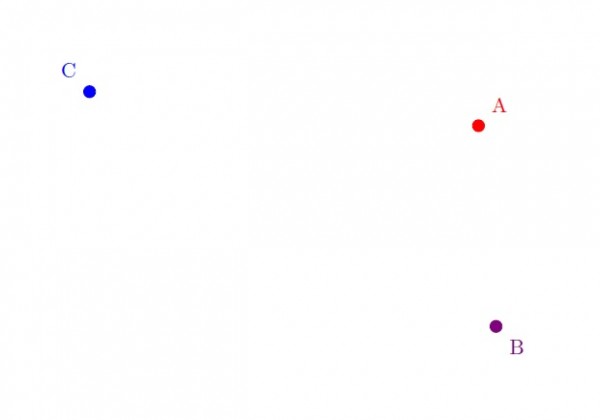
Noktalarımıza A, B ve C diyelim.
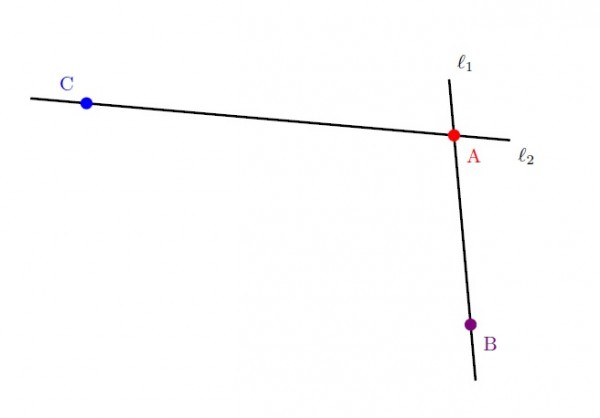
İki farklı noktadan, tanımı gereği, biricik bir doğru geçer. Bu bilgiyi kullanırsak
A ve B noktalarından geçen biricik bir $\ell_1$ dogrusu
A ve C noktalarından geçen biricik bir $\ell_2$ dogrusu
vardır.
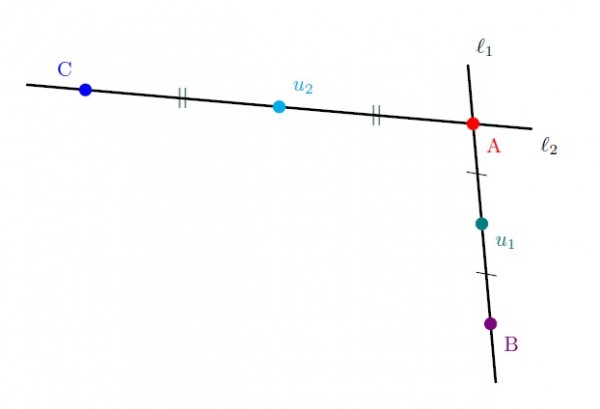
İki noktanın, tanımı gereği, biricik bir orta noktası vardır ve bu noktalar ile aynı doğru üzerindedir. Bu bilgiyi kullanırsak
A ve B noktalarının biricik bir $u_1$ orta noktası
A ve C noktalarının biricik bir $u_2$ orta noktası
vardır. Bu noktalar, sırası ile, $\ell_1$ ve $\ell_2$ üzerindedir.
Bir doğruya bir noktası üzerinde dik olan biricik bir doğru vardır.
$\ell_1$ doğrusuna $u_1$ noktasından geçen biricik bir dik $L_1$ doğrusu
$\ell_2$ doğrusuna $u_2$ noktasından geçen biricik bir dik $L_2$ doğrusu
vardır.
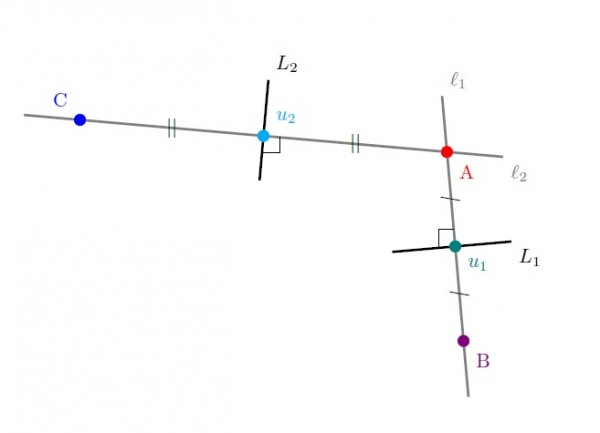
İki farklı noktaya eşit mesafede olan noktalar bu noktaların orta noktasından geçen ve bu iki nokta arsındaki doğruya dik olan doğru üzerindedir; ve bunlardan başka bu şartı sağlayan nokta yoktur. Bu nedenle çemberin merkezi hem $L_1$ hem de $L_2$ üzerinde olmalıdır.
$A$, $B$ ve $C$ doğrusal olmadığından $\ell_1$ ve $\ell_2$ paralel doğrular değildir. Paralel olmayan doğruların dikleri de paralel değildir. Bu nedenle $L_1$ ve $L_2$ doğruları da paralel değildir.
Paralel olmayan iki doğru biricik bir noktada kesişirler. Bu bilgi ile $L_1$ ve $L_2$ doğruları biricik bir $O$ noktasında kesişir, ve bu nokta $A$, $B$ v e $C$ noktalarına eşit uzaklıktadır.
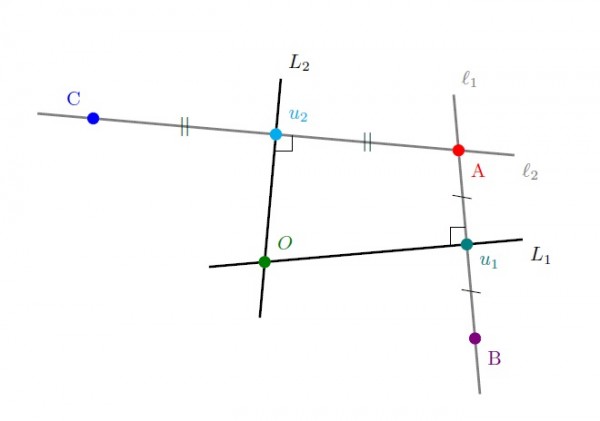
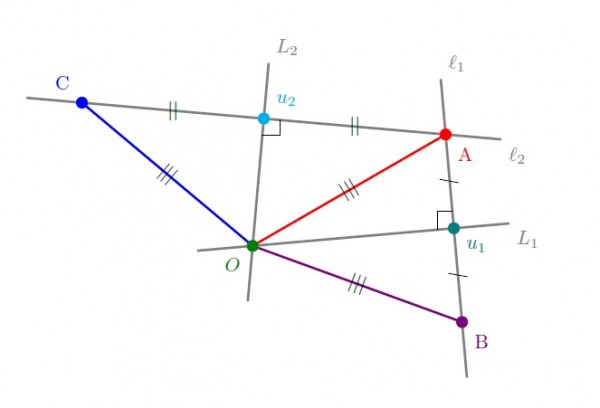
Bu sonuçlar gereği çemberin merkezi olmaya aday tek nokta $O$ noktasıdır. Bu noktaya $|OA|=|OB|=|OC|$ mesafeli noktaların oluşturduğu çember kümesi, doğal olarak, $A$, $B$ ve $C$ noktalarından geçer.