Basit faizin ve birleşik faizin matematiksel tanımını vermeden önce bir örnek ile anlatalım ve ikisinin farkını gözlemleyelim.
Diyelim ki başlangıçta sahip olduğunuz ana para olarak $100$ TL paranız var ve buna yılda $\%10$ getiri ile faiz alacaksınız. Paranızı yatırdığınız birinci yılın sonunda paranıza ek olarak $$100\times \frac{10}{100}=10$$ TL faiz getirisi elde edersiniz ve toplam da $$100+10=110$$ TL paranız olur.
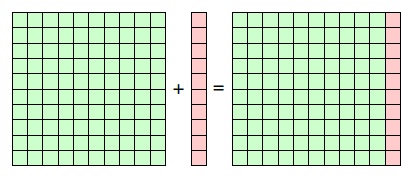
 Bu bir yılın sonunda basit faiz veren kuruluş ana paranızı $100$ TL olarak düşünmeye devam ederken birleşik faiz veren kuruluş ana paranızı $100$ TL olarak değil de $110$ TL olarak düşünür.
Bu bir yılın sonunda basit faiz veren kuruluş ana paranızı $100$ TL olarak düşünmeye devam ederken birleşik faiz veren kuruluş ana paranızı $100$ TL olarak değil de $110$ TL olarak düşünür.
Ana paranız $100$ TL olarak düşünüldüğünde tekrardan $100$ TL için $10$ TL daha getiriniz olur ve toplamda $$110+10=120$$ TL para sahibi olursunuz.
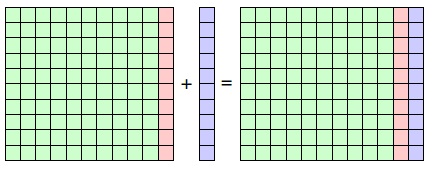

Birleşik faizde ise ana paranız $110$ TL olarak düşünüldüğünden $\%10$luk faizinizi $110$ TL üzerinden $$110\times \frac{10}{100}=11$$ TL olarak alırsınız. İkinci yılın sonunda ise toplam da $$110+11=121$$ TL paraya sahip olursunuz.
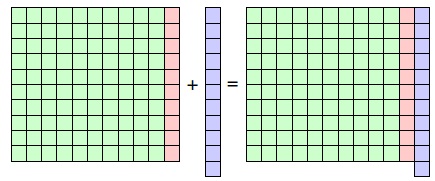

Gördüğünüz üzere birinci sene değişen bir durum olmasa da ikinci sene nisbeten biraz fazla para kazandık. İki senede kazandığımız ek $1$ TL'yi belki küçümseyebilirsiniz. Aradan koskoca iki sene geçmiş ve ekten sadece $1$ TL getiri elde edilmiş. İki sene için cüzi sayılacak ek bir gelir elde etsek de uzun vadede birleşik faiz basit faize oranla ciddi bir ek kazanç getirir.
Basit faizde her sene sabit olarak $10$ TL ek gelir elde ederken birleşik faizde her sene bir önceki seneki paranın $1+\frac{10}{100}=1.1$ katı kadar kazanırız. Bu durumda $n$ yıl sonra basit faizde $$100+10\cdot n$$ TL kazanırken birleşik faizde $$100\cdot1.1^n$$ TL para kazanırız.
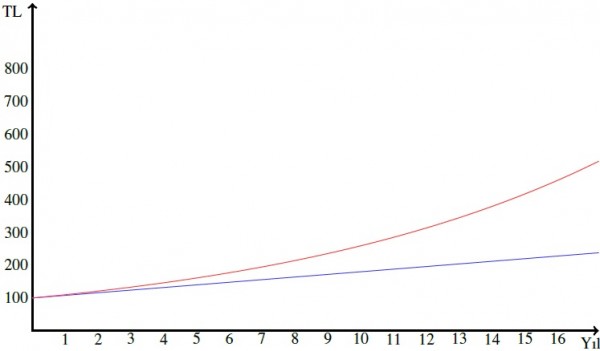
Senaryomuzu birkaç yıl daha ileriye götürürsek $100$ TL ana para koyduğumuzda gelecekte bunun ne kadar olabileceğini tablodaki ve grafikteki gibi görebilirsiniz.
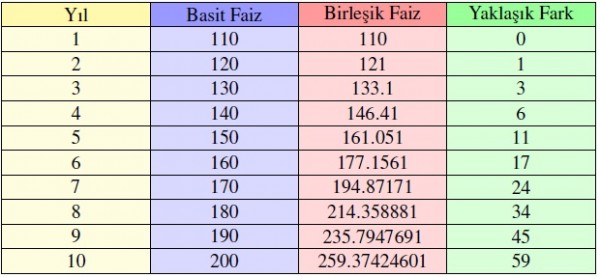
Düzenli Basit Faiz: $A$ ve $x$ negatif olmayan gerçel sayılar ve $n$ bir pozitif tam sayı olsun. $A$ miktar ana paraya yıllık $\%x$ düzenli basit faiz getirisi ile $n$ yılda $$A\cdot\left(1+n\cdot \frac{x}{100}\right)$$ kadar olur.
Düzenli Birleşik Faiz: $A$ ve $x$ negatif olmayan gerçel sayılar ve $n$ bir pozitif tam sayı olsun. $A$ miktar ana paraya yıllık $\%x$ düzenli basit faiz getirisi ile $n$ yılda $$A\cdot\left(1+\frac{x}{100}\right)^n$$ kadar olur.
Basit Faiz: $n$ bir pozitif tam sayı, $A$ ve $x_1,\ldots,x_n$ negatif olmayan gerçel sayılar olsun. $A$ miktar ana paraya yıllık, sırası ile, $\%x_1,\ldots,\%x_n$ basit faiz getirisi ile $n$ yılda $$A\cdot\left(1+ \frac{x_1}{100}+\ldots+ \frac{x_n}{100}\right)$$ kadar olur.
Birleşik Faiz: $n$ bir pozitif tam sayı, $A$ ve $x_1,\ldots,x_n$ negatif olmayan gerçel sayılar olsun. $A$ miktar ana paraya yıllık, sırası ile, $\%x_1,\ldots,\%x_n$ birleşik faiz getirisi ile $n$ yılda $$A\cdot\left(1+\frac{x_1}{100}\right)\cdots\left(1+\frac{x_n}{100}\right)$$ kadar olur.
Not: Faiz tanımının doğasında pozitiflik ve geleneğinde yüzde vardır. Tanımı genişleterek faizi sıfır ya da negatif alabiliriz. Bunun yanısıra birde ya da binde gibi başka oranlara da bakabiliriz. Bir mağaza bir ürünün fiyatına oransal bir azaltma yaptığında bunun adı indirim olarak geçer. Faiz yerine göre farklı isimler de almaktadır.