Bu cevabı limitin geometrik anlamı üzerine verdiğimi belirteyim. Bu nedenle yoruma dayalı bir cevap olacaktır.
Problemi geometrik olarak anlama:
Problem geometrik olarak aşağıdaki taralı alanı soruyor.
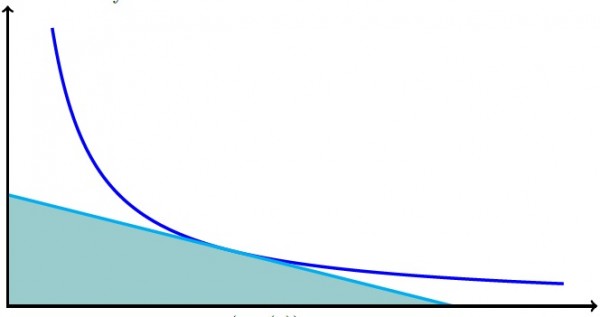
Çözüm için bir yaklaşım:
$(a,f(a))$ noktalasından geçen sekant doğrularının "limiti" olarak $\ell$ doğrusunu bulmaya çalışacağız.
Bunun için $(a,f(a))$ noktasından geçen sekant doğrularının eğimleri ile ilğileneceğiz ve $\ell$ doğrusunun eğimini bulmaya çalışacağız.
$(a,f(a))$ noktasından geçen $\ell$ doğrusunun eğimini bulursak $\ell$ doğrusunun denklemini de bulabiliriz.
Bu bilgi ile $\ell$ doğrusunun eksenleri kestiği noktaları bulabiliriz ve dik üçgenin alan hesabı ile de sonuca varırız.
a noktasından geçen sekant doğrularını tanımlama:
$h\ne 0$ olmak üzere $\ell_h$ sekant eğrisini $f$ fonksiyonun oluşturduğu eğri üzerindeki $(a,f(a))$ ve $(a+h,f(a+h))$ noktalarından geçen doğru olarak tanımlayalım.
a noktasından geçen sekant doğrularının eğimlerini bulma:
$h\ne 0$ olmak üzere $\ell_h$ eğrisinin eğimi \begin{align*}\frac{f(a+h)-f(a)}{(a+h)-a}\ &=\ \frac{f(a+h)-f(a)}{h}\\[16pt]&=\ \frac1h\cdot \left(f(a+h)-f(a)\right)\\[16pt]&=\ \frac1h\cdot \left(\frac1{a+h}-\frac1a\right)\\[16pt]&=\ \frac1h\cdot \frac {a-(a+h)}{a\cdot(a+h)}\\[16pt]&=\ \frac1h\cdot \frac {-h}{a\cdot(a+h)}\\[16pt]&=\ \frac {-1}{a\cdot(a+h)}\end{align*} değerine eşit olur.
Limit fikri ile teğet doğrusunun eğimini bulma:
$a+h$ değeri ne kadar $a$ değerine yakınsa, yani $h$ değeri $0$ değerine ne kadar yakınsa, $\ell_h$ doğrusun teğet doğrusuna o kadar yakın olur; eğimleri yaklaşır.
$h$ değeri sıfıra yaklaştıkça $\ell_h$ doğrusuna karşılık gelen eğimler $$\frac {-1}{a\cdot(a+0)}=-\frac1{a^2}$$ değerine yaklaşır. Bu değer de teğet doğrusunun eğimi olur.
Teğet doğrusunun denklemini bulma:
Teğet doğrusu $\left(a,\frac1a\right)$ noktasından geçen ve eğimi $-\frac1{a^2}$ olan doğru olduğundan denklemi $$y-\frac1a=-\frac1{a^2}\left(x-a\right)$$ olur.
Teğet doğrusunun $y$ eksenini kestiği noktanın ordinatını bulma:
Bu nokta bir $c$ gerçel sayısı için $(0,c)$ formunda olmalıdır. Bu nokta doğru üzerinde olduğundan doğrunun denklemini sağlar; yani $$c-\frac1a=-\frac1{a^2}\left(0-a\right)$$ eşitliği sağlanır. Bu denklemden $$c=\frac2a$$ olduğunu buluruz.
Teğet doğrusunun $x$ eksenini kestiği noktanın apsisini bulma:
Bu nokta bir $d$ gerçel sayısı için $(c,0)$ formunda olmalıdır. Bu nokta doğru üzerinde olduğundan doğrunun denklemini sağlar; yani $$0-\frac1a=-\frac1{a^2}\left(d-a\right)$$ eşitliği sağlanır. Bu denklemden $$d=2a$$ olduğunu buluruz.
Oluşan dik üçgenin alanını bulma:
$(0,0)$, $(0,2a)$ ve $\left(0,\frac2a\right)$ noktalarının oluşturduğu dik üçgenin dik kenar uzunlukları $2a$ ve $\frac2a$ olduğundan bu üçgenin alanı, yani bizden istenen bölgenin alanı, $$\frac12\cdot 2a\cdot \frac2a=2$$ olur.
Hoş bir sonuç:
Bu problemin cevabı $a$ değişkeninden bağımsız olarak bir sabit sayıya eşittir. Hangi noktadan teğet çizersek çizelim eksenlerle sınırlanan alan hep $2$ değerine eşit olur.