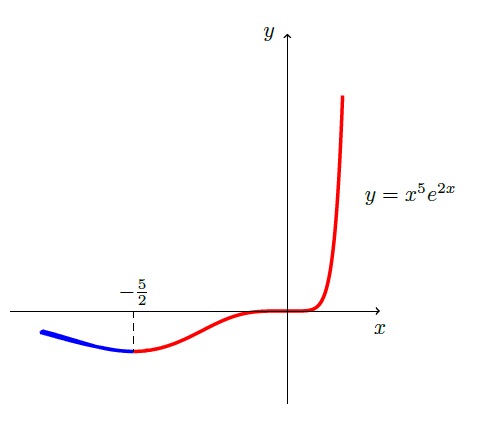
Fonksiyonun türevi:
$f$ fonksiyonun türev kuralı $$f^\prime(x)=5x^4\cdot e^{2x}+x^5\cdot 2e^{2x}= e^{2x}\cdot x^4\cdot (5+2x)$$ olur.
Türevi sıfır yapan değerler:
Çarpanları ayrı ayrı inceleyelim.
$e^{2x}$ her $x$ gerçel sayısı için pozitif değerler alır.
$x^4$ ifadesi sadece $x=0$ olduğundan sıfır değerini alır.
$5+2x$ ifadesi sadece $x=-5/2$ olduğundan sıfır değerini alır.
Türevin işaretini inceleme:
Çarpanları ayrı ayrı inceleyelim.
$e^{2x}$ her $x$ gerçel sayısı için pozitif değerler alır.
$x^4$ ifadesi $x<0$ ya da $x>0$ olduğunda pozitif değerler alır.
$5+2x$ ifadesi $x<-5/2$ olduğunda negatif $x>-5/2$ olduğunda pozitif değerler alır.
Bu bilgileri birleştirsek
$x<-5/2$ olduğunda $f^\prime(x)$ değerleri negatif olur.
$-5/2<x<0$ olduğunda $f^\prime(x)$ değerleri pozitif olur.
$x>0$ olduğunda $f^\prime(x)$ değerleri pozitif olur.
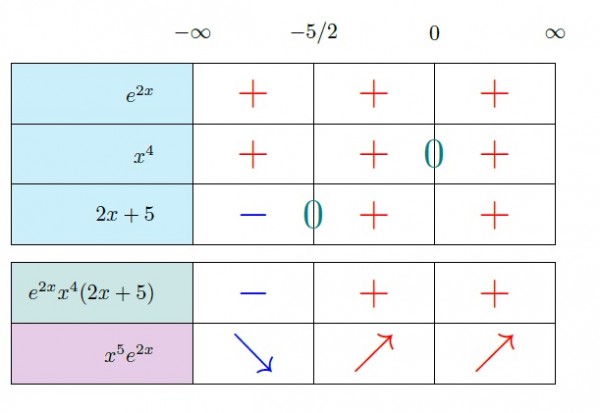
Fonksiyonun artan olduğu açık aralıkları bulma:
$f$ fonksiyonu türevinin pozitif olduğu açık aralıklarda artandır. Ayrıca karşılık gelen kapalı aralıkta sürekli ise, ortalama değer savı gereği, bu kapalı aralık üzerinde de artandır. Bu nedenle $$(-5/2,0] \ \ \ \text{ ve } \ \ \ [0,\infty)$$ kapalı aralıkları üzerinde $f$ fonksiyonu artan olur, ve bu ikisinin birleşimi olan $$(-5/2,\infty)$$ açık aralığı üzerinde de artan olur.
Ayrıca $f$ fonksiyonu $(-\infty,-5/2)$ aralığı üzerinde azalan olduğundan bu fonksiyonun artan olduğu biricik en geniş açık aralık $(-5/2,\infty)$ aralığı olur.