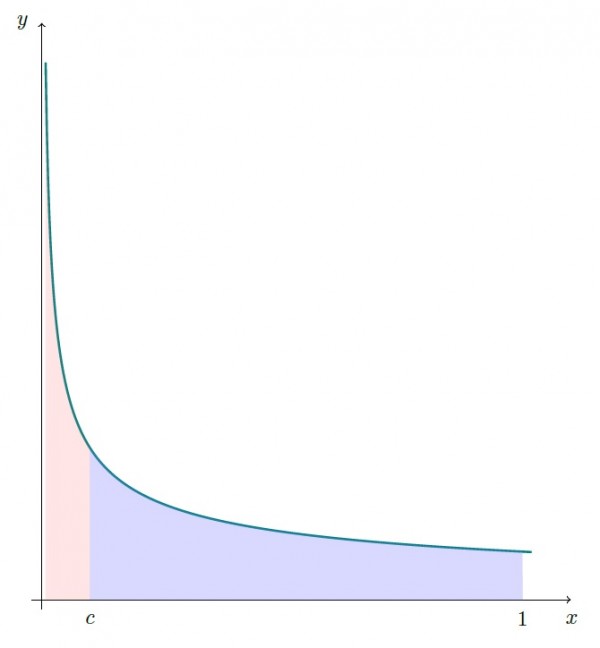
Has olmayı bozan noktalar:
$1/\sqrt x$, $(0,1]$ aralığı içerisindeki herhangi bir kapalı aralık üzerinde, sürekli olduğundan, sınırlı bir fonksiyondur.
Ayrıca $0$ noktasındaki sağ limiti $\infty$ olduğundan has olmanın bir koşulu olan sınırlı olma koşulunu bozmuş oluruz.
Has olmayan integrali has olan integrallerin limiti olarak yazma:
$0^+$ yaklaşımı içerisindeki tüm integraller ayrı ayrı has integrallerdir. Has olmayan integralin tanımı gereği $$\int_0^1\frac1{\sqrt x}dx=\lim\limits_{c\to0^+}\int_{c}^{1}\frac 1{\sqrt x} dx$$ integralleri ve bunların limiti ile ilgilenmeliyiz.
İntegralleri hesaplama:
İç integrali hesaplarsak\begin{align*}\int_{c}^{1}\frac 1{\sqrt x} dx \ &= \ \int_{c}^{1} x^{-\frac12} dx \\[7mm] &= \ 2x^{\frac12} \bigg |_c^1 \\[7mm] &= \ 2-2\sqrt c \end{align*} sonucunu elde ederiz.
Limit alma ve sonuç:
Elde ettiğimiz bilgiyi kullaırsak \begin{align*}\int_0^1\frac1{\sqrt x}dx \ &= \ \lim\limits_{c\to0^+}\int_{c}^{1}\frac 1{\sqrt x} dx\\[7mm] &= \ \lim\limits_{c\to0^+}\left(2-2\sqrt c \right)\\[7mm] &= \ 2-2\sqrt 0\\[7mm] &= \ 2\end{align*}eşitliğini elde ederiz.