Soruyu tek değişkenli fonksiyona çevirme:
Kestiğimiz eş karelerin bir kenar uzunluğunu $x$ cm olarak alırsak ayrıtları $$x, \ \ \ 18-2x, \ \ \ 18-2x$$ olan bir dikdörtgenler prizması elde ederiz.

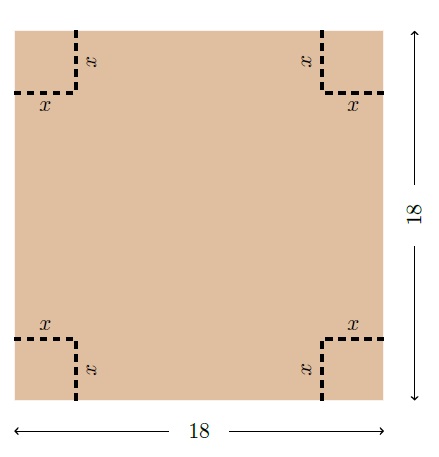
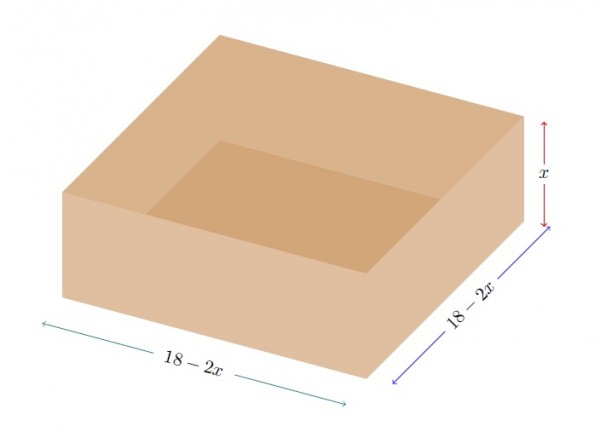
Bu prizmanın hacmi \begin{align*}&x\cdot (18-2x)\cdot (18-2x)\\[10pt] &\ = \ x\cdot \left(18^2-2\cdot 18\cdot 2x+(2x)^2\right)\\[10pt] &\ = \ 324x-72x^2+4x^3\text{ cm}^3\end{align*} olur.
Ayrıt uzunlukları pozitif gerçel sayılar olduğundan $x$ ve $18-2x$ sayıları pozitif olmalıdır; yani $$0<x<9$$ eşitsizliği sağlanmalıdır.
Bu bilgilerle sorumuz \[f \ \colon \ \left\{\begin{array}{r c l} (0,9) &\rightarrow& \mathbb R_+ \\[10pt]x &\mapsto& 324x-72x^2+4x^3\end{array}\right.\] fonksiyonunun en büyük değerini bulmak oluyor.
Bulduğumuz fonksiyon ile ilgilenme:
Fonksiyonun türevini alırsak her $x\in(0,9)$ değeri için $$f(x)=324-144x+12x^2 = 12 \cdot (27-12x+x^2) = 12 \cdot (x-3)\cdot (x-9)$$ olur ve bu ifade, aralık içerisinde, sadece $x=3$ için sıfıra eşit olur.
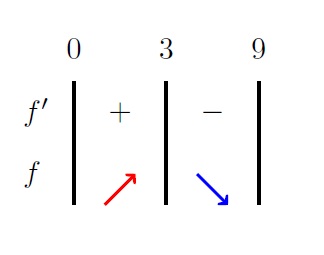
Bu bilgiler gereği $f$ fonksiyonunun en büyük değeri $$f(3)=3\cdot (18-2\cdot 3)\cdot (18-2\cdot 3)=432$$ olarak alır ve istenen şartlardaki bir kutunun en büyük iç hacmi $$432\text{ cm}^3$$ olur.