$\sin$ ve $\cos$ sürekli fonksiyonlardır.

Question

$a$ gerçel sayısı olmak üzere $\sin$ ve $\cos$ fonksiyonları $a$ noktasında süreklidir.

Answer 1

Sıfır civarında trigonometrik bir eşitsizlik elde etme:
$0<a<1$ olduğunda çember üzerinde $a$ kadar ilerlediğimizde çember yayının uzunluğu $a$ olur. Bu çember yayı dik kenarları $\sin a$ ve $1-\cos a$ olan dik üçgenin hipotenüsünden büyük olduğundan dik kenarların ikisinden de büyük olur; yani  $$\sin a<a \ \ \ \text{ ve } \ \ \ 1-\cos a<a$$ eşitsizlikleri sağlanır.

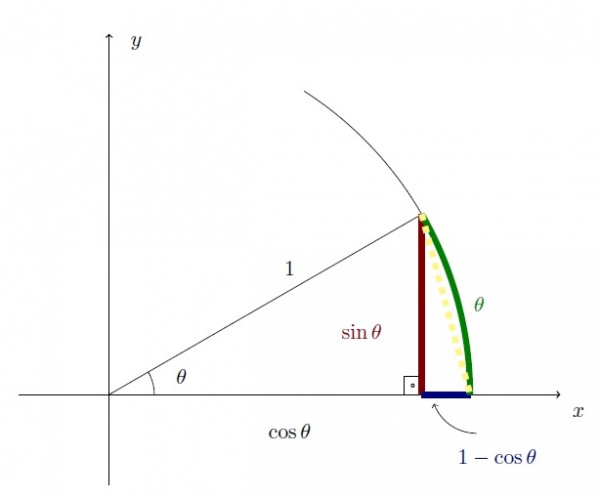
$-1<a<1$ olduğunda $\sin (-a)=-\sin a$ ve $\cos (-a)=\cos a$ ile $\sin 0=0$ ve $\cos 0=1$ olduğunu kullanırsak $$|\sin a|\le |a| \ \ \ \text{ ve } \ \ \ | 1-\cos a|\le |a|$$ eşitsizliklerini elde ederiz.

Süreklilik tanımı ile sıfır noktasında sürekliliği gösterme:
$\epsilon>0$ verilsin. $\delta=\min\{\epsilon,1\}>0$ seçersek $|x-0|< \delta$ olduğunda \begin{align*}&|\sin x-\sin 0|=|\sin x|\le |x|<\epsilon \ \ \ \text{ ve }\\[10pt] &|\cos x-\cos 0|=| 1-\cos x|\le |x|<\epsilon\end{align*} eşitsizlikleri sağlandığından $\sin$ ve $\cos$ fonksiyonları $0$ noktasında sürekli olurlar.

Her noktada sürekliliği gösterme:
$a$ bir gerçel sayı olsun. Sıfır noktasındaki süreklilikleri kullanarak\begin{align*} \lim\limits_{h\to 0}\sin (a+h)\ &=\ \lim\limits_{h\to 0}(\sin a\cdot\cos h+\cos a\cdot \sin h)\\[10pt]&=\ \sin a\cdot1+\cos a\cdot 0\\[10pt]&=\ \sin a\end{align*} eşitliğini ve \begin{align*} \lim\limits_{h\to 0}\cos (a+h)\ &=\ \lim\limits_{h\to 0}(\cos a\cdot\cos h-\sin a\cdot \sin h)\\[10pt]&=\ \cos a\cdot1-\sin a\cdot 0\\[10pt]&=\ \cos a\end{align*} eşitliğini elde ederiz. Bu eşitlikler bize $\sin$ ve $\cos$ fonksiyonlarının sürekli olduğunu verir.

Answer 2

Sıfır noktasında sürekliliği göstermek için sürekliliğin tanımı yerine limit özelliklerini de kullanabiliriz.

Limit özelliklerini kullanarak sıfır noktasında sürekliliği gösterme:
$[-1,1]$ aralığı üzerinde $$0\le |\sin x|\le |x| \ \ \ \text{ ve } \ \ \ 0\le | 1-\cos x|\le |x|$$  eşitsizlikleri sağlandığından ve $\lim\limits_{x\to 0}0=\lim\limits_{x\to 0}|x|=0$ olduğundan, sıkıştırma savı gereği, $$\lim\limits_{x\to 0}|\sin x|=0 \ \ \  \text{ ve } \ \ \ \lim\limits_{x\to 0} | 1-\cos x|=0$$ eşitlikleri sağlanır. Mutlak limiti sıfır olan fonksiyonların limitleri sıfır olur. Bu nedenle $$\lim\limits_{x\to 0}\sin x=0 \ \ \  \text{ ve } \ \ \ \lim\limits_{x\to 0} (1-\cos x)=0$$ eşitlikleri sağlanır. Elde ettiğimiz $$\lim\limits_{x\to 0}\sin x=0=\sin 0 \ \ \  \text{ ve }$$$$\lim\limits_{x\to 0} \cos x=\lim\limits_{x\to 0}((1-\cos x)+1)=0+1=1=\cos 0$$ eşitlikleri bize $\sin$ ve $\cos$ fonksiyonlarının $0$ noktasında sürekli olduğunu verir.